分类结果差异的统计检验
2017-07-10 MacLearn machine-learning feature-selection对于一个分类任务,在进行 特征选择+交叉验证 时,通常会需要比较实用不同的特征集或者不同的特征选择算法得到的结果是否有显著差异。如果只是比较交叉验证得到的平均正确率,比如使用特征集 A 得到的average accracy是 72%,而使用特征集 B 得到的average accuracy是 73%,这 1% 的差异无法说明特征集 A 相对于特征集 B 的优越性是统计显著的。差异可能源于随机误差,也许你换一个交叉验证的随机数这个差异就没有了。因此,需要借助统计方法比较结果之间是否有显著差异,从而证明你的特征或者特征选择算法确实是很棒棒的。
以常用的十折交叉验证(10-fold cross-validation)为例, 每一折都会得到accuray,一共得到10个accuracy结果。对同一数据集,分别使用使用特征选择算法 t1和 t2,得到的交叉验证结果如下表所示:
| Algorithm | Accuracy | Algorithm | Accuracy | |
|---|---|---|---|---|
| t1-fold1 | 81% | t2-fold1 | 75% | |
| t1-fold2 | 81% | t2-fold2 | 75% | |
| t1-fold3 | 85% | t2-fold3 | 75% | |
| t1-fold4 | 82% | t2-fold4 | 80% | |
| t1-fold5 | 81% | t2-fold5 | 80% | |
| t1-fold6 | 77% | t2-fold6 | 80% | |
| t1-fold7 | 80% | t2-fold7 | 76% | |
| t1-fold8 | 80% | t2-fold8 | 81% | |
| t1-fold9 | 85% | t2-fold9 | 75% | |
| t1-fold10 | 79% | t2-fold10 | 76% |
其中t1-average-accuray=81%, t2-average-accuracy=77%。对上面两列accuracy进行 配对t检验 (Paired t-test),得到统计显著性为 p=0.021 (p<0.05),如下图所示(use SPSS)。
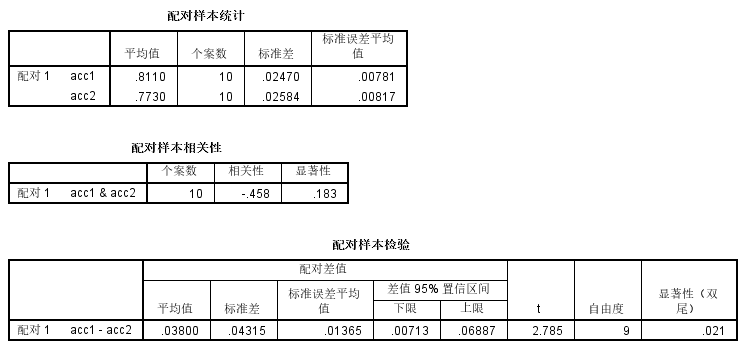
此时我们可以认为算法 t1 是显著优于 t2 的。如果经过分析 p>0.05,则不能得出这样的结论。
如果需要对比3种以上不同的特征选择算法或者特征集,这时候统计方法的使用就有些许改变。以十折交叉验证(10-fold cross-validation)为例,同一数据集,3种不同的特征选择算法 f1, f2, f3。此时需要进行 f1-f2, f2-f3, f1-f3 三组配对t检验。因为进行了多次比较(multiple comaprison),此时p值必须进行校正,小于校正后的p值才能认为具有统计显著性。比如使用 Bonferroni adjustment。由于进行了3次比较,p值需要除以3 (0.05/3),即 p<0.017 时才能认为具有统计显著性。
常用的交叉验证方法除了10-fold-CV,还有 LOOCV (Leave-one-out cross-validation)。而LOOCV是每次得到一个测试样本的预测标签,将整个数据集循环过一遍之后得到一个最终的结果(accuray/sensitivity/specificity),而不是像10-fold-CV那样得到一个结果序列,这时候Paired t-test显然不适用了,那么这时候该怎么进行统计检验以比较不同算法的差异呢?
参考之前读过的一篇文章[1],其使用LOOCV进行交叉验证,然后用 McNemar’ test 计算不同方法得到的accuracy的统计差异。这种方法使用分类结果的标签(二分类变量),而不是accuracy(连续变量)来计算统计差异。这样的话可以先用LOOCV得到对每个样本的预测标签(predicted label),每一种方法得到一组预测标签结果,然后再根据原始标签(ground truth label)对比不同方法的结果差异。其实 McNemar’s test 跟 Paired t-test 非常类似,只是用来计算统计量的变量有二分或是连续之差别。
P.S.
- 除了使用 Paired t-test,还可以使用 ANOVA with repeated measure 分析不同方法的统计差异。
- 对比AUC间的差异一般使用 Delong’s test,也有一篇文章用 Permutation test [2]。
有的时候会遇到这种情况,比如你使用方法 t1 得到的average accuracy是 85%,而使用方法 t2 得到的average accuracy是 70%, 这时候会觉得方法 t1 肯定显著优于 t2。然而经过统计检验,居然 p»0.05。这到底是为什么呢?这时候调出交叉验证每一折(each fold)的结果一看便知,造成没有显著差异的原因大抵是结果的方差比较大,比如某一折的accuracy是90%,而另一折的accuracy直接掉到了30%。而造成交叉验证的结果方差如此之大的原因可能是训练数据太少,或者是类不平衡问题严重。
Summary
- 应用LOOCV,对比不同特征集或算法得到结果的差异可用以下统计方法:
- 应用10-fold-CV,对比不同特征集或算法得到结果的差异可以用以下统计方法:
- 对比AUC差异:
Reference
[1] Structural imaging biomarkers of Alzheimer’s disease: predicting disease progression | Neurobiology of aging, 2015
[2] Machine learning framework for early MRI-based Alzheimer’s conversion
prediction in MCI subjects | Neuroimage, 2015
[3] Laerd Statistics
[4] Bonferroni adjustment

Comments